 nucalc.exe
nucalc.exe

이번 수능 B형(홀수형) 30번 문제이다. (가)조건을 이용하면 f(x)가 ax(x-1) 라는 것을 얻을 수 있고, 이에 (나)조건을 이용하면-k=-1 일때 접선의 개수가 2개밖에 되지 않는다는 사실을 이용한다.- a=e 라는 사실을 얻는다. 별로 어려운 문제는 아니나 실제 수능 시험장에서는 많은 학생들이 어려움을 느낄법 하다. 다항함수와 지수함수의 곱을 두번이나 미분하고, 경우나누기도 들어가는 데다가 (나)와 같은 조건이 낯설게 다가온다는 것은 분명 정답률을 낮추는데 크게 기여한다. 하지만 그럼에도 결코 어려운 문제는 아니다. 학생들에게 하는 표현 그대로 쓰자면 '그냥 풀면 풀린다.'
푸는 과정에서 그래프를 그려 보는 것은 큰 도움이 된다. 시간이 많이 들게 되는 문제가 있기 때문에 실전에서는 꼭 필요한 부분만 그리기를 권하지만, 다 끝난 이후에 복기할때는 꼭 그려보기를 제안한다.
다음 그림은 이 문제와 관련된 그래프들이다.

보라색으로 표시된 그래프는 완성된 g(x) 이다. 실전에서 그리는 팁은 e^x나 e^-x 는 함수값의 부호를 그대로 유지시킨다(모든 곳에서 양수값이므로)는 것과 다항식과 곱했을때 그 극한이 결국 지수함수대로 간다, 다르게 표현하면 다항식을 '씹어 먹는다.'는 것을 이용한다. 이 문제에서라면, 다항함수랑 비슷하되(0과 1에서 근을 갖는 이차함수) x가 무한대로 가는 극한값은 0+라는 것이다.
파랑색 그래프는 마지막에 얘기하도록 하자. 빨강, 초록, 에메랄드 색 직선 세개는 k=1/2 경우의 접선들을 나타낸 것이다. 근사치로 넣어서 정확히 접하진 않지만 (나) 조건을 이해하는데 도움이 될 것이다.
파랑색 그래프의 정체는 다음과 같다. 중간에 등장하는 수식들이나 기타 논리의 흐름을 반드시 당신의 언어로 종이에 손으로 직접 옮겨보라. 그냥 이 글을 읽는 것은 하등의 도움도 되지 않는다.
우선 g(x)의 임의의 점 (x,g(x)) 에서의 접선의 방정식을  라고 둔 뒤에
라고 둔 뒤에 
와 연립을 하자. l(x)가 접선의 방정식이므로 (x,g(x))에서 둘의 함수값과 순간 기울기는 같다. 따라서 식 두개를 얻는다.


이 두 식을 연립하면  를 얻는다. 그리고 (나) 조건을 다시 보자. -1 < k < 0 일때 접선의 개수가 3 이라고 했으므로, 서로 다른 m1, m2, m3 에 대해서
를 얻는다. 그리고 (나) 조건을 다시 보자. -1 < k < 0 일때 접선의 개수가 3 이라고 했으므로, 서로 다른 m1, m2, m3 에 대해서  가 g(x)와 접해야 한다. 그러므로
가 g(x)와 접해야 한다. 그러므로  의 근이 -1 < k < 0 일때, 그리고 오직 그때만 3개여야 한다.
의 근이 -1 < k < 0 일때, 그리고 오직 그때만 3개여야 한다.  는 y=0 에서 접하고, 그 위로는
는 y=0 에서 접하고, 그 위로는  는 3개 이상의 근을 가질 수 없다. 그리고 마찬가지로 파란색 그래프에서 보이듯 두번째 극점과 그 아래로는 3개 이상의 근을 갖지 못한다.
는 3개 이상의 근을 가질 수 없다. 그리고 마찬가지로 파란색 그래프에서 보이듯 두번째 극점과 그 아래로는 3개 이상의 근을 갖지 못한다.  를 미분해보면 x=1 이 두번째 극값이라는 사실을 얻고, 그때의 값이 -1이 됨을 우리는 알고 있다.(왜 그런지 모르겠다면 더 고민해보기를..) 따라서 a = e 를 얻는다. 파란색 그래프는
를 미분해보면 x=1 이 두번째 극값이라는 사실을 얻고, 그때의 값이 -1이 됨을 우리는 알고 있다.(왜 그런지 모르겠다면 더 고민해보기를..) 따라서 a = e 를 얻는다. 파란색 그래프는  를 나타낸 것이다. 이제 그 정체를 깨닫게 됐을 것이다.
를 나타낸 것이다. 이제 그 정체를 깨닫게 됐을 것이다.
중간에 헷갈리기 시작한 독자들이 있을 것이다. 헷갈렸다면 우선 혼자서 위에를 이해할 수 있도록 10분은 고민해보기를 바란다. 아래는 중간에 tricky한 부분을 수정한 것이다. 두 가지가 사실은 같은 얘기를 하고 있다는 것을 깨닫는 것이 독자의 미지수와 함수에 대한 이해를 높이는데 큰 기여를 할 것이라 믿는다.
우선 g(x)의 임의의 점 (t,g(t)) 에서의 접선의 방정식을  라고 둔 뒤에
라고 둔 뒤에 와 연립을 하자. l(x)가 접선의 방정식이므로 (t,g(t))에서 둘의 함수값과 순간 기울기는 같다. 따라서 식 두개를 얻는다.
와 연립을 하자. l(x)가 접선의 방정식이므로 (t,g(t))에서 둘의 함수값과 순간 기울기는 같다. 따라서 식 두개를 얻는다.

l'(t)=  = g'(t)
= g'(t)
이 두 식을 연립하면  를 얻는다. 그리고 (나) 조건을 다시 보자. -1 < k < 0 일때 접선의 개수가 3 이라고 했으므로, 고정된 한 k에 대해 서로 다른 m1, m2, m3 가 존재하여
를 얻는다. 그리고 (나) 조건을 다시 보자. -1 < k < 0 일때 접선의 개수가 3 이라고 했으므로, 고정된 한 k에 대해 서로 다른 m1, m2, m3 가 존재하여  가 g(x)와 접해야 한다. 그러므로
가 g(x)와 접해야 한다. 그러므로  의 근이 -1 < k < 0 일때, 그리고 오직 그때만 3개여야 한다. 따라서
의 근이 -1 < k < 0 일때, 그리고 오직 그때만 3개여야 한다. 따라서  이므로
이므로  는 y=0 에서 접하고, y 가 그 이상일때
는 y=0 에서 접하고, y 가 그 이상일때  는 3개 이상의 '근'을 가질 수 없다. 그리고 마찬가지로 두번째 극점과 그 아래로는 3개 이상의 근을 갖지 못한다.(파란색 그래프의 개형을 한번 보라.)
는 3개 이상의 '근'을 가질 수 없다. 그리고 마찬가지로 두번째 극점과 그 아래로는 3개 이상의 근을 갖지 못한다.(파란색 그래프의 개형을 한번 보라.)  를 미분해보면 x=1 이 두번째 극값이라는 사실을 얻고, 그때의 값이 -1이 됨을 우리는 알고 있다.(왜 그런지 모르겠다면 더 고민해보기를..) 따라서 a = e 를 얻는다. 파란색 그래프는
를 미분해보면 x=1 이 두번째 극값이라는 사실을 얻고, 그때의 값이 -1이 됨을 우리는 알고 있다.(왜 그런지 모르겠다면 더 고민해보기를..) 따라서 a = e 를 얻는다. 파란색 그래프는  를 나타낸 것이다. 이제 그 정체를 깨닫게 됐을 것이다.
를 나타낸 것이다. 이제 그 정체를 깨닫게 됐을 것이다.
아! a 가 양수일때/음수일때 두가지로 케이스 분류하는 것도 잊지 말기를 바란다. 실제 시험에서는 양수로 두면 풀릴텐데, 시험 볼때는 그냥 넘어더라도 나중에 따로 공부할때는 음수로 가정해보고 풀어보아야 한다.
일부러라도 덜 자세하게 썼으니 잘 모르겠는 부분을 만났을때는 고민하는 시간으로 쓸 수 있기를... 의문이 가는 사항이 있다면 댓글 달아주시기를! 혹시 보고 있는 고3들이 있다면 수고했다는 말과 함께 지금은 이런 글을 찾아볼 떄가 아니라 즐겁게 놀때라는 것을 말해주겠습니다. 이 글은 이제 수능을 준비하는 학생들을 위해 쓰여진 글입니다.
같이 있는 프로그램은 그래프 그리는 프로그램입니다. 수학에서도 '실험'이 얼마나 중요한지 얘기하고 싶은데, 제가 많은 학생들을 만날 기회가 없어서 찬 안타깝네요.(물론 본래 공부보다 시간을 더 쏟게 되는건 실험이 아닙니다.) 어떤 방법으로던 도움이 필요하다는 요청을 받게 된다면 최선을 다해서 도와드리겠습니다. 공부하는 틈틈이 이러면 어떨까 저러면 어떨까 그래프도 그려보고 다르게 가정도 해보고 문제를 만나보길 바랍니다. 평화!
는 행렬의 곱셈을 이항연산으로 갖는 group이다. (하략)
를 G의 center(중심군)라고 부른다.
이다.
의 임의의 원소 A와
의 임의의 원소 B에 대하여 AB = BA가 성립해야한다. 이때 B는 임의의 가역행렬이므로 기초 행렬(elementary matrix)여도 상관없다. 따라서 첫째로 B가 i-번째 열의 a배를 j-번째 열에 더하는 기초 행렬 연산에 대응하는 기초 행렬이었다고 가정하자. 이때, 기초 행렬을 오른쪽에 곱하는 것은 동일한 연산을 행에 대해서 시행하는 것임이 잘 알려져 있으므로, AB 는 A 의 i 번째 행의 a 배를 j 번째 행에 더한 행렬임을 안다. 따라서 AB = BA 는 i-번째 행의 a배를 j-번째 행에 더한 것과 i 번째 열의 a배를 j-번째 열에 더한 것과 같다는 뜻이므로 A가 대각 행렬(diagonal matrix)이어야만 함을 함의한다. (왜 그런가?) 둘째로 B가 i-번째 열과 j-번째 열을 바꾸는 기초 행렬 연산에 대응하는 기초 행렬이었다고 가정하자. 기초 행렬 연산을 오른쪽에 행하는 것은 그 연산을 열에 행하는 것과 같음이 잘 알려져있고, 따라서 AB는 A의 i 번째 행과 j 번째 행을 바꾼 행렬임을 안다. 이때 BA는 A의 i 번째 행과 j 번째 열을 바꾼 행렬이고, A는 대각 행렬이므로 A의 i-번째 행(열)의 원소와 A의 j-번째 행(열)의 원소는 서로 같아야 한다. 따라서 A는 모든 성분이 같은 대각 행렬이고 이는 항등 행렬(Identity matrix)의 상수배로 나타낼 수 있다는 것과 같은 말이다. 증명 끝.

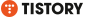
 nucalc.exe
nucalc.exe
