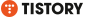군의 연산표와 두가지 의문
(모든 정의는 이인석, <선형대수와 군>의 것을 따른다.)
G={1,x_2,x_3,...} 라고 놓을 때, group G의 연산표를 다음과 같이 정의한다.(티스토리는 별 기능을 다 제공한다.)
|
1 |
x_2 |
... |
x_j |
... |
1 |
1 |
x_2 |
... |
x_j |
... |
x_2 |
x_2 |
|
|
|
|
... |
... |
|
|
... |
|
x_i |
x_i |
|
... |
x_ix_j |
... |
... |
|
|
|
... |
|
관찰 11.2.9. (Cancellation Law) x,y,z ∈ G 일 때, xy = xz 이면 y = z 이다. 또, xz = yz 이면, x = y 이다.
관찰 11.2.14. 연산표의 각 가로줄에는 모두 다른 원소가 나타난다. 각 세로줄도 마찬가지이다.
증명 : xy = xz 이면, Cancellation Law 에 의해 y = z 이므로.
관찰 11.2.15. 고정된 x ∈ G 에 대해서, 함수 λ_x : G -> G 를
λ_x(y) = xy, (y ∈ G)
로 정의하면, λ_x : G -> G는 bijection 이다. 더 고상하게 말하면, λ_x는 집합 G를 permute한다.
(※ λ(람다)는 left multiplication 에서 첫 글자를 따온 것이다. 마찬가지로 right multiplication은 ρ(로)로 표기한다.)
증명 : 그 말이 그 말. 아차, 지금은 surjectivity 도 보여야 한다.
쭉쭉 읽고 써보다가 첫번째 든 의문은 다음과 같다. injectivity만 보여도 surjectivity가 보여지지 않는가? 즉, 어차피 G의 원소는 한정되어 있는데 서로가 달라야 한다면 모든 G의 원소들이 '선택받아야'하는 것 아닌가? 그리고 나서 다시 전으로 돌아와서 살펴보니 다른 의문이 들었다. 11.2.15. 에서는 left multiplication에 대해서만 보였는데 G가 가환(commutative)하지 않다면 증명이 불충분한 것이 아닌가? 즉, 가로줄 증명은 되었으나 세로줄 증명은 안된 것이 아닌가?
첫번째 의문이 들었을때 가장 먼저 생각난 것이 dimension theorem이다. 그런데 곰곰히 생각해보니 λ_x가 선형이라는 것은 대체 무슨소리인가 싶은 것이다. 아, 그것이 중요한게 아니었다. 왜 dimension theorem에 의해 injectivity가 surjectivity를 보증하는가? 바로 비둘기집의 원리(pigeon hole principle)때문이었다. 그렇다면 비둘기집의 원리에 의해 surjectivity를 보이지 않아도 충분한가? 우선은 '그렇지 않다.' 이 책에서 언급된(4.3.4) 비둘기집의 원리는 유한 집합에 한정되어 있다.(cardinality가 생각나긴 했는데 아직 배우질 않아서 언급은 하지 않겠다.) 그리고나서 살펴보니 dimension theorem을 이용해 증명한 부분도 f.d.v.s.(finite dimensional vector space)에 한정되어 있었다. 따라서, '유한군에서는 비둘기집의 원리에 의해 bijection 임을 알 수 있지만, 무한군에 대해서는 surjectivity를 직접 증명해줘야 한다.'
두번째 의문을 보고 책에 주어진 연산표들을 살펴보니 모두 가환군의 연산표라서 의미가 없었다. 그리고 또 생각을 해보니 비가환군에도 관찰 11.2.14.가 적용되므로 어차피 연산표를 봐봐야 당연히 의미가 없을 것이라는 것을 알게 되었다. 아무튼 곰곰히 생각해봐도 세로줄 증명은 관찰 11.2.14.의 끝에 '마찬가지이다.'라는 말로 갈음된 것 같다. 즉, xz = yz 이면 x = y 라는 사실과 right multiplication 이 bijection 이라는 사실에서 새로이 얻어야 하는 것 같다. 나도 모르겠다.
'수학 > 대수학' 카테고리의 다른 글
| 일반 선형군의 중심군(center of general linear group) (0) | 2013.11.18 |
|---|---|
| John Hannah, <A Geometric Approach to Determinants> : 행렬식에 대한 기하학적 접근 (0) | 2013.06.21 |
| isomorphic이란? (2) | 2013.04.23 |